SEMum_NA14
The model file can be downloaded from IRIS EMC
Citations and DOIs
To cite the original work behind this Earth model:
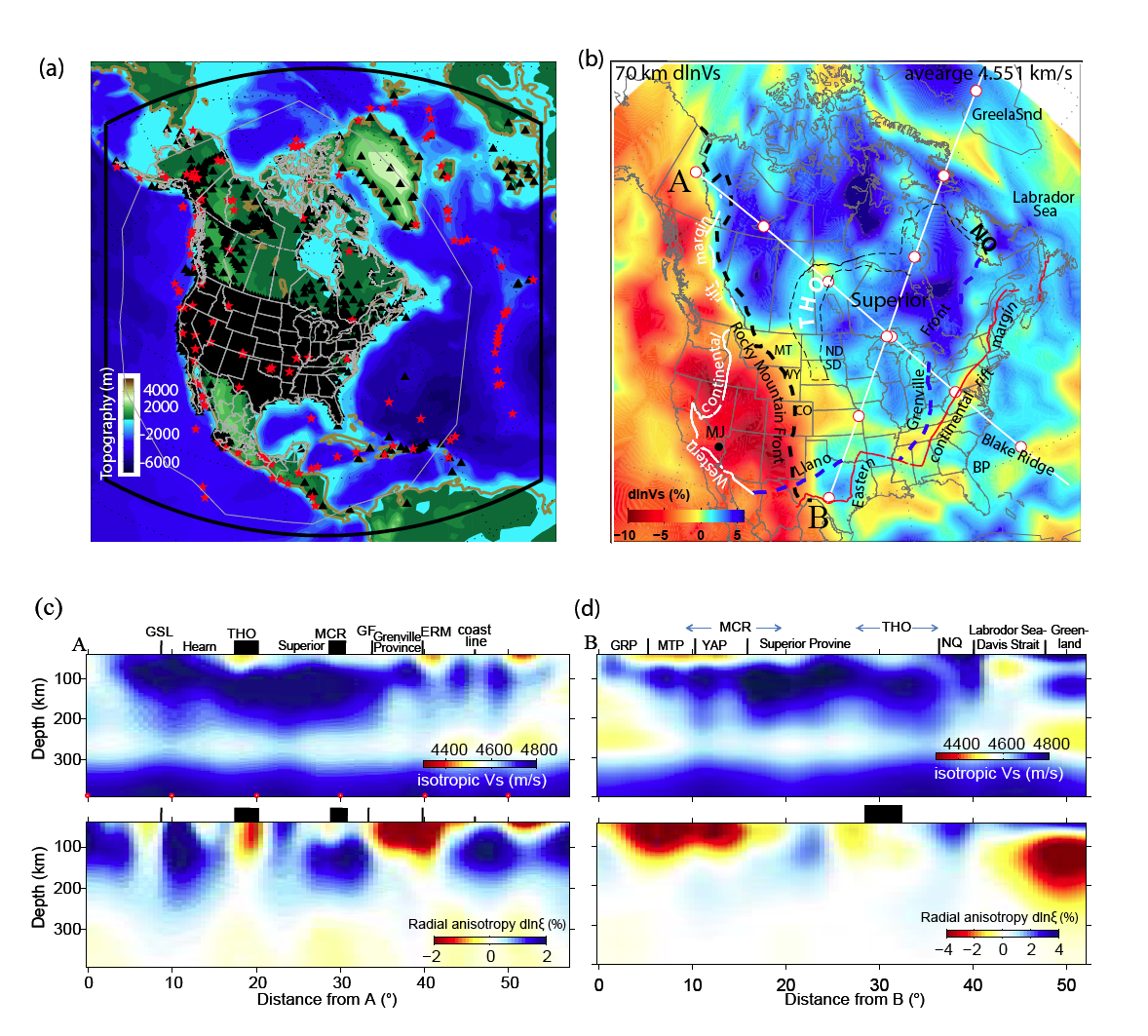
- Yuan, H., French, S., Cupillard, P., Romanowicz, B., 2014. Lithospheric expression of geological units in central and eastern North America from full waveform tomography. Earth Planet Sc Lett. 402, 176–186, https://doi.org/10.1016/j.epsl.2013.11.057.
References
- Cupillard Cupillard, P., Delavaud, E., Burgos, G., Festa, G., Vilotte, J.-P., Capdeville, Y., Montagner, J.-P., 2012. RegSEM: a versatile code based on the spectral element method to compute seismic wave propagation at the regional scale. Geophys. J. Int. 188, 1203-1220.
- French, S.W., Romanowicz, B.A., 2014. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography. Geophys. J. Int. 199, 1303-1327.
- Lekić, V., Romanowicz, B., 2011. Inferring upper-mantle structure by full waveform tomography with the spectral element method. Geophys. J. Int. 185, 799-831.
- Li, X., Romanowicz, B., 1996. Global mantle shear velocity model developed using nonlinear asymptotic coupling theory. J. Geophys. Res 101, 22245-22273.
- Li, X.-D., Romanowicz, B., 1995. Comparison of global waveform inversions with and without considering cross-branch modal coupling. Geophys. J. Int. 121, 695-709.
- Montagner, J.-P., Griot-Pommera, D.-A., Lave, J., 2000. How to relate body wave and surface wave anisotropy? J. Geophys. Res. 105, 19,015-019,027.
- Romanowicz, B., Yuan, H., 2012. On the interpretation of SKS splitting measurements in the presence of several layers of anisotropy. Geophys. J. Int. 188, 1129-1140.
- Yuan, H., French, S., Cupillard, P., Romanowicz, B., 2014. Lithospheric expression of geological units in central and eastern North America from full waveform tomography. Earth Planet Sc Lett. 402, 176–186.